
 |
Eager Space | Videos | All Video Text | Support | Community | About |
|---|

A commonly asked question is "why don't they just fly starship and super heavy from Boca Chica to Florida?"
Let's see whether that's possible...

I did a video on shipping Starship and Super Heavy by sea.
Our goal is to get both Starship and Super Heavy from the factory in Boca Chica, Texas to Pad 39A on Kennedy Space Center without using a barge.

The distance between the launch site at Boca Chica to Pad 39A in Florida is 1660 km.
The question is really whether both Super Heavy and starship can make it there, but starship is a lot heavier with its fins and thermal protection tiles, while Super Heavy is mostly just a big tube with a lot of engines. This means that, for most purposes, the question is whether starship can make it because it has less performance than super heavy.
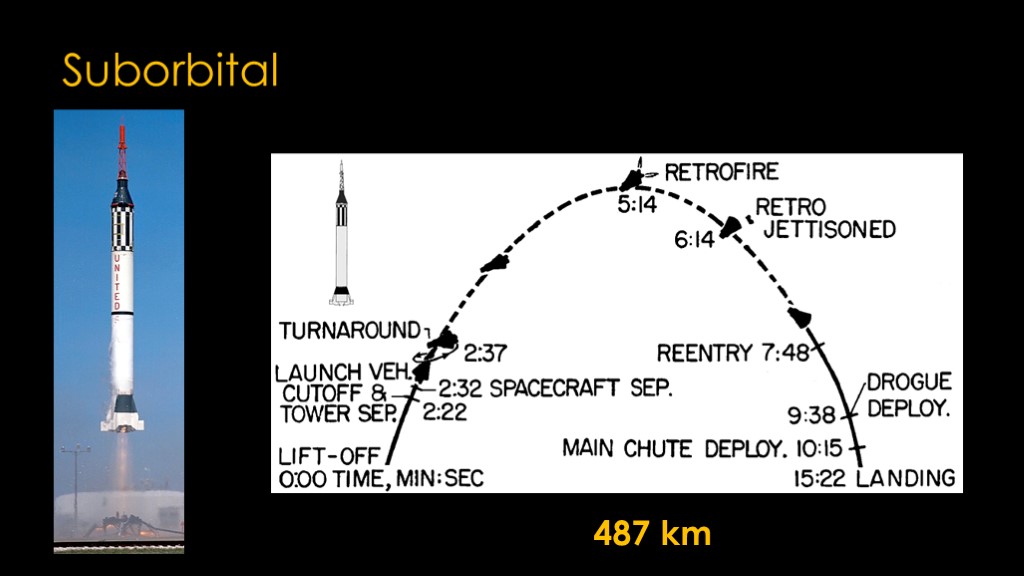
Can we do it with a suborbital flight, the way that the first two Mercury launches did? The first Mercury launch landed 487 kilometers downrange from the launch site.
That seems promising...

Here's my plan of attack to answer this question:
Step 1: Figure out the delta v required to make the trip. I'll put a link to a video that talks more about delta v, but it's basically the way we quantify how hard it is to get from one location in space to another.
Step 2: Compare that to an estimated delta v for starship. I have that from some earlier work.
Step 3: Go on a bike ride, because this isn't going to take more than a few hours.

The math for this is well understood; it's determined by the ballistic equation.
If we known how far away the target is we can calculate the delta-v required to get there.
Here's the equation; you can see the delta v is equal to the speed at launch...
That seems incorrect...
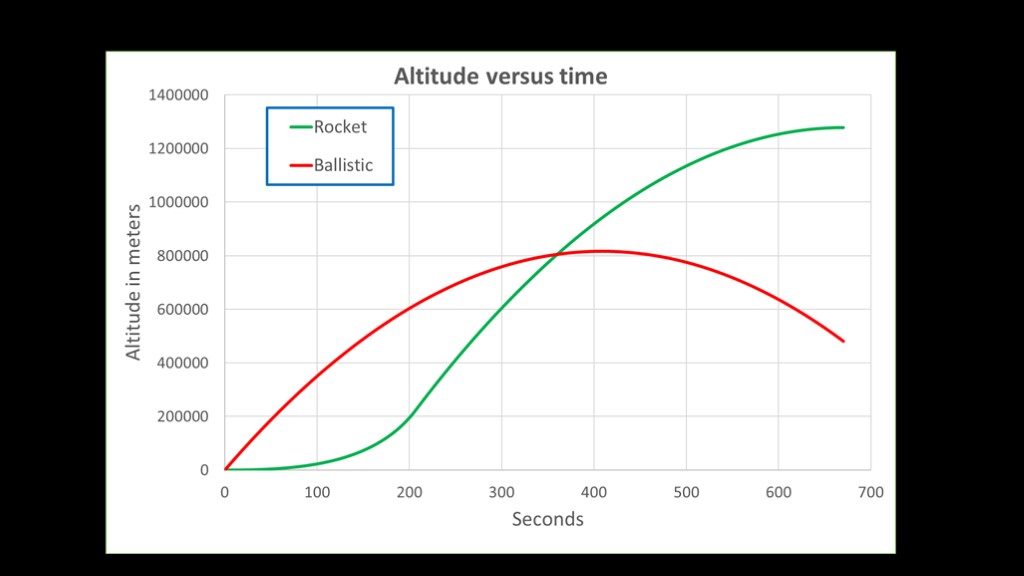
Here's a graph that shows a ballistic trajectory in red and a rocket trajectory in green. We can see that they are quite a bit different.
Ballistic trajectories start with their highest velocity at launch and then the only forces on them are gravity and air resistance (this chart ignores air resistance).
Rockets start at a velocity of zero and accelerate faster as they get lighter.
Ballistic trajectories have nothing to do with rocket launches, and those equations don't apply.

Time to move to plan B.
Plan B is to write a physics simulation of a rocket launch. I had been gradually moving towards this for some of the earlier videos, doing some fun stuff in Excel.
Once the simulation is there, we can plug in the values we have for starship - the dry weight, the propellant capacity, the engine thrust, etc. These are of course all *estimates*.
We then specify how full the fuel tanks are.
The simulator will then try different flight paths and find the one that gives us the maximum horizontal distance.
Note that this doesn't consider air resistance, so it's somewhat flawed. Maybe version 2 will support that.
I'm testing 200 different trajectories to see which one is best, and that's very easy to code and very hard to Excel, so I wrote a program. The simulator is written as a pretty junky Windows Forms program using C#.
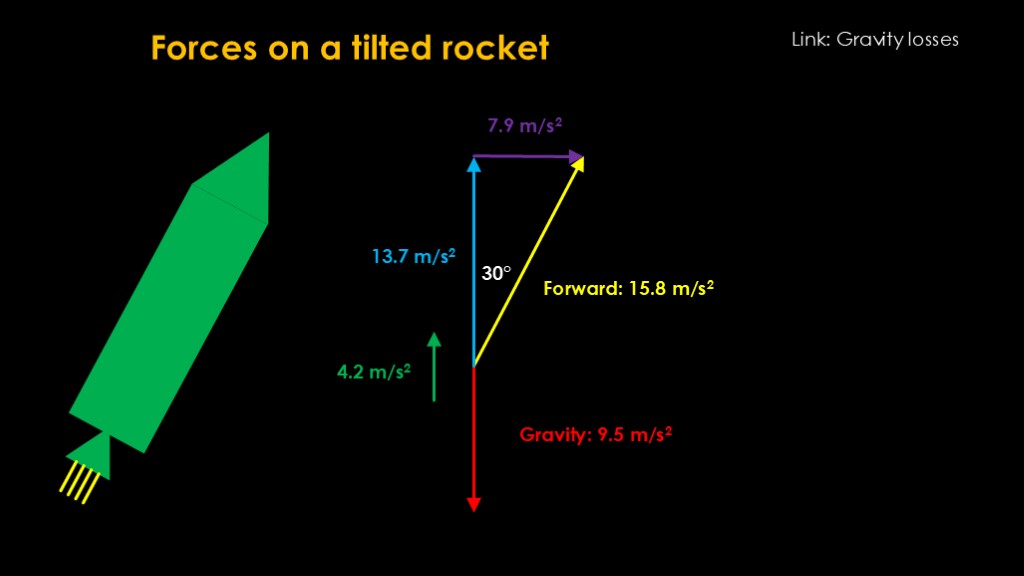

This simulation is fairly simple. We want to track the time and the sideways and upwards components of the distance in meters, the velocity in meters per second, and the acceleration in meters per second squared. Here's how it works.
We start at time zero, and since we are sitting on the launch pad, we have no distance or velocity. We will start with step #3, where, based on the approach in the last slide, we figure out the sideways and upwards acceleration. At launch, the rocket is pointing straight up so there is no sideways acceleration and the upwards acceleration is 2.4 meters per second squared.
Time is now 1 second into the flight
We now go to step #1, where we update the velocity based on the acceleration the previous second. Looking at time zero, we take the side and up accelerations and add them to the previous side and up velocities (both zero), so we now have a side velocity of zero and an up velocity of 2.4 meters per second.
Finally, we do step #2, where we update the distance based on the velocity. The up velocity went from 0 to 2.4 meters per second. That means the *average* velocity was half of that, or 1.2 meters per second. In one second, that means we travelled 1.2 meters, so that is the up distance.
And back to step #3. The rocket is no longer pointed quite straight up, so we have a side velocity of 0.05 and an up velocity of 2.46.
Onto time = 2 seconds. The velocity is easy to update; we just add the acceleration to the current velocity and get 0.05 meters per second to the side and 4.86 meters per second up.
Update the distance. The sideways distance is the average of the current velocity and the previous velocity, or 0.025. The up distance is the average of 2.4 and 4.86 *plus* the previous up distance of 1.2, or 4.83 as the up distance.
Update the acceleration again, now 0.11 and 2.52.
Time equals 3 seconds.
Add the accelerations to the existing velocities to get 0.16 and 7.38, and finally the side distance is increased by 0.105, giving us 0.13. The up distance is increased by 6.12, and adding that to the existing distance gives us 10.95
This process continues every second. As I noted in the gravity loss video, the acceleration will continue as long as the engines keep burning, and then we just end up with gravity as our main force.
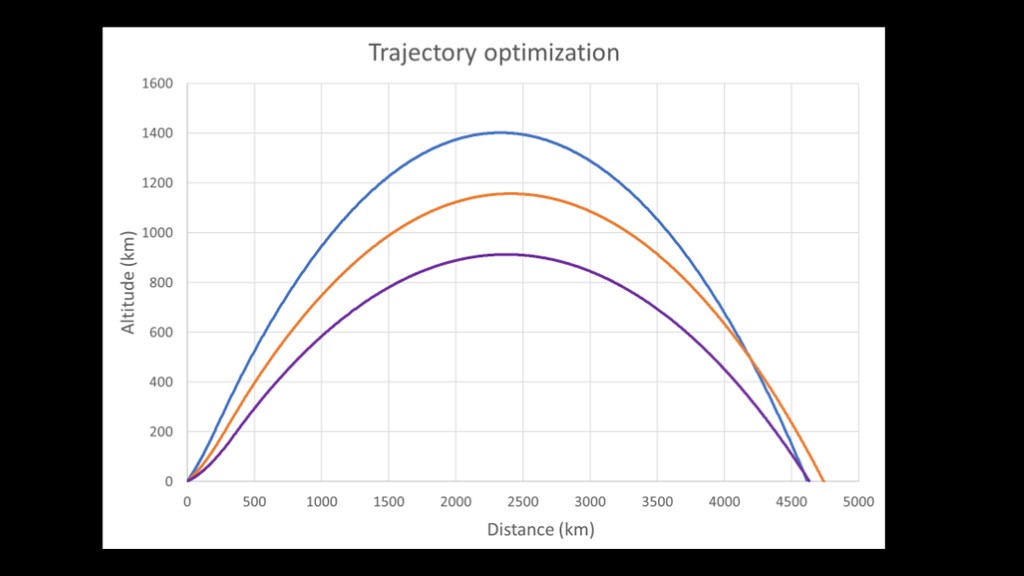
Here's an example of three trajectories out of the 200 the simulator evaluates.
The top blue one gets the most altitude, but that means less horizontal velocity and therefore less distance.
The bottom purple one spends the most on horizontal velocity and goes the fastest but it doesn't stay up long enough to get a lot of distance.
The middle golden one balances out altitude and horizontal velocity and manages to get a bit more distance than the other options.

A few assumptions built into the results...
First, it assume starship has 3 sea level engines and 6 vacuum engines and they are all running. Starship cannot get off the ground with a full fuel load with 6 engines, so this is a fair assumption
Second, the raptors are only putting out 1800 kN of thrust. That's at the low end of where they will be, and it does not factor in thrust improvements, higher thrust in vacuum, or higher ISP of vacuum engines.
Third, the simulation does not attempt to model drag. I figured that with the conservative choices on the engines that air resistance would not be significant.
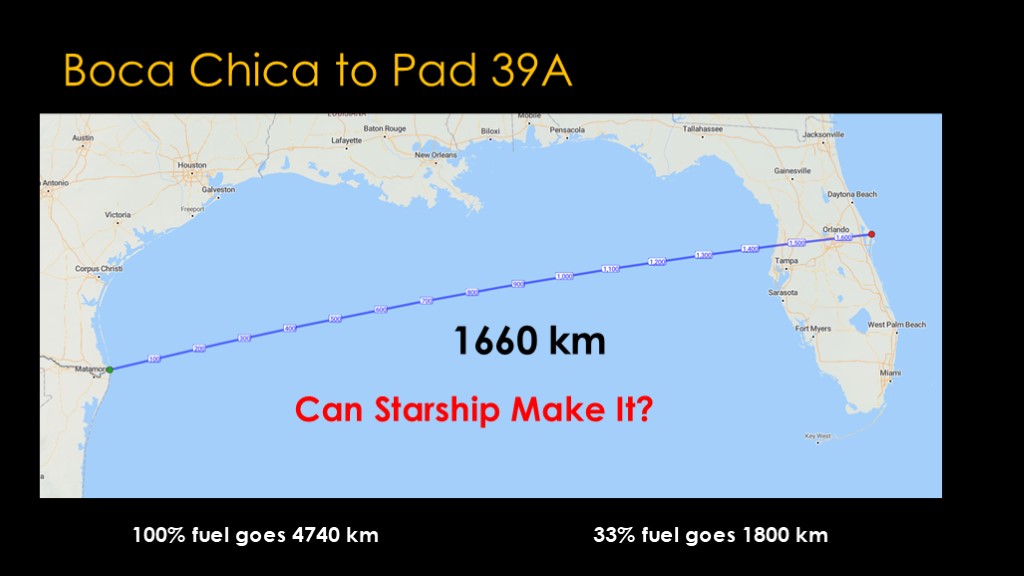
There's a problem
As starship launches, the impact zone if something goes wrong will proceed along the flight path.
There are a number of people who would be unhappy to be put at risk, including Disney World, Universal Studios, and the 8 million people who live on or near the flight path.
It's therefore very unlikely that the FAA would allow such a flight with an unproven rocket.

Sigh
Direct flights are out, so the answer to the question is "starship can't make the hop".

Then I got an idea.
I got a wonderful, awful idea.

We need a dogleg.
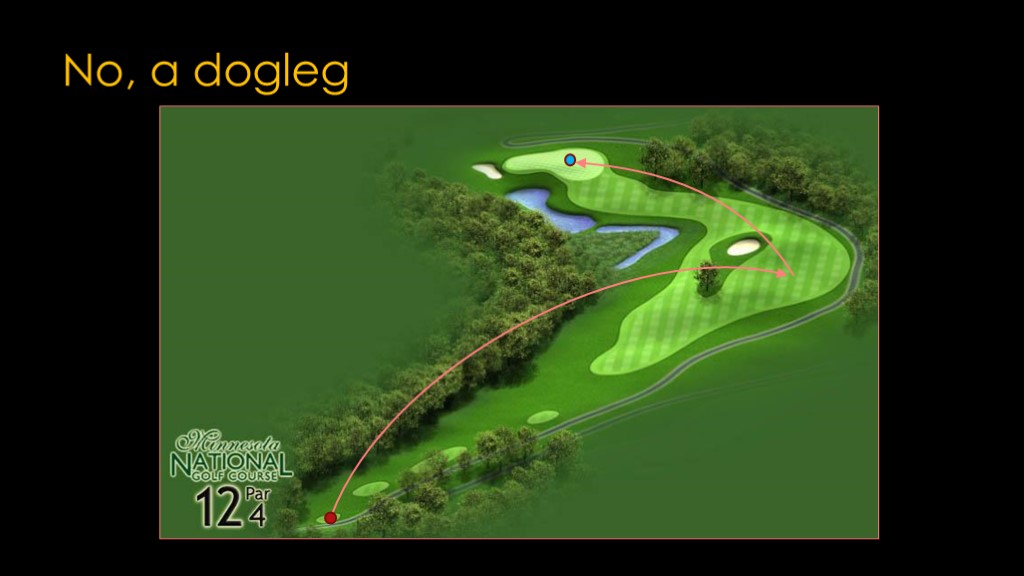
No, a dogleg.
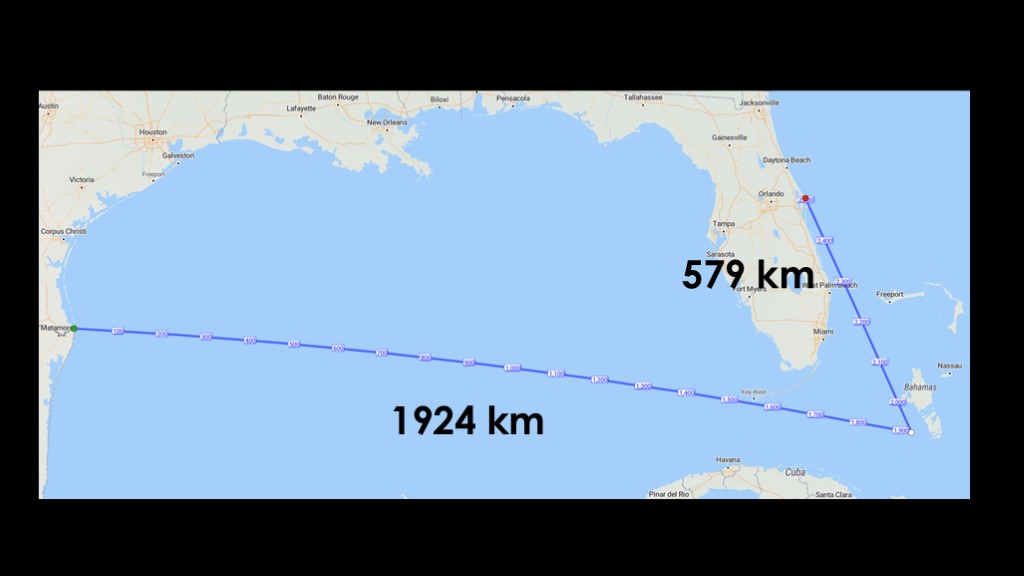
We can do this trip in two legs.
One hop south of the Florida keys ending just off the Bahamas, and then a second hop back to the north to land at kennedy space center.

The obvious way to do this is pretty simple. You take one of the mobile launch platforms SpaceX has been working on, and you park it near the Bahamas. Hop to the platform, check everything out, refuel, and then hop to the cape. Simple and straightforward.
That requires the platform to be functional, of course.
Is there a way to do this without a platform?
Maybe...
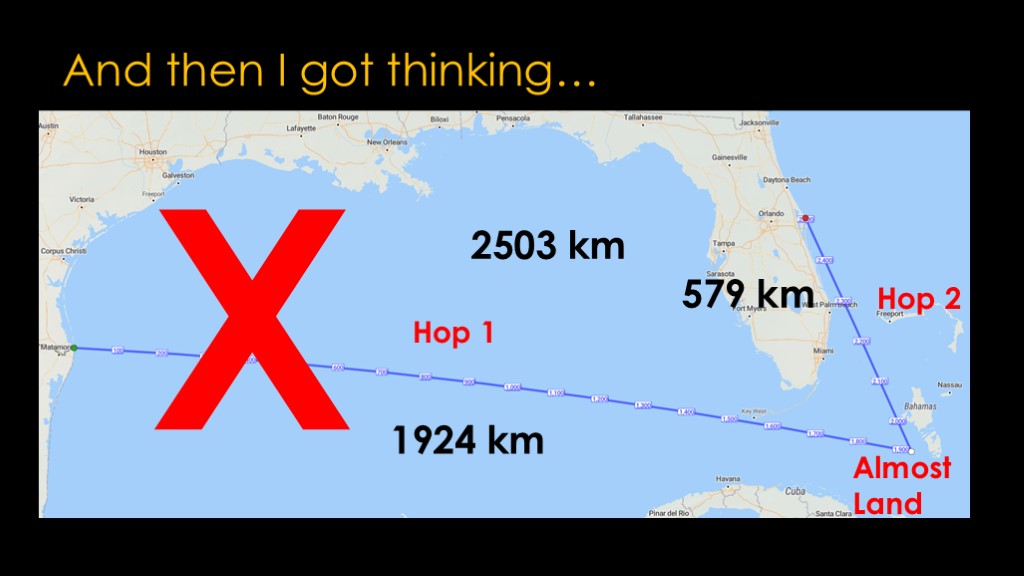
Can you do this with two hops sequentially?
Do hop 1 from Boca Chica, almost land at the position near the Bahamas, then take off and do hop 2 and land at Kennedy Space Center.
That would be about 2500 km of total distance, and that's a lot less than the 4700 km I said starship could do, so it's easy, right?
Unfortunately, that math isn't correct
Let's explore why.
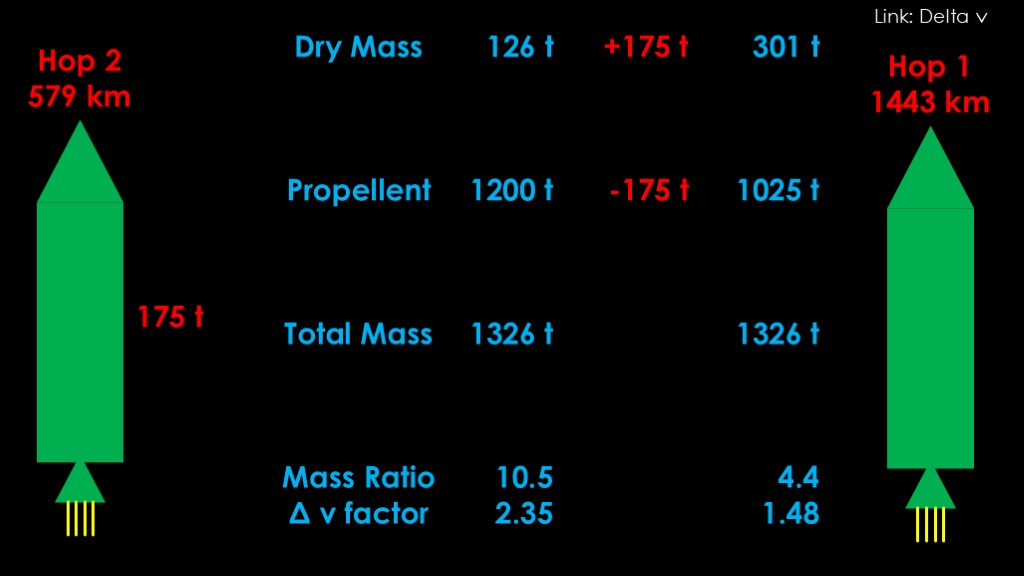
The second hop is 579 km, and the simulator tells me that Starship will need 175,000 kilograms - or 175 tons - of propellant to make that hop. That's how much propellant we need left after the first hop.
Let's look at some numbers for starship. Once again, these are all estimates, and specifically this assumes starship that has not been stretched longer.
The dry mass is 126 tons and starship carries 1200 tons of propellant, making the total mass 1326 tons. That gives us a mass ratio of 10.5 and a delta v factor of 2.35.
If you want to understand more about delta v, here's a link to another video
How does this change if we need to reserve 175 tons of fuel for the second hop? That will add 175 tons to the dry mass and subtract 175 tons from the propellant mass
That gives us a dry mass of 301 tons, and that takes our mass ratio all the way down to 4.4 and the delta v factor down to 1.48. That's a lot less than 2.35.
Running the simulator, that gives us a hop 1 distance of 1443 km. That's a lot less than the 1924 km that we need.

How can we fix that?
What if the raptors have 2000 kilonewtons of thrust instead of 1800? That gets us 1562 kilometers, still not enough.
What if starship is stretched? We don't know what the details are, but that's probably not enough
What if starship can use its fins to glide farther? Maybe, bur probably not.
I don't think these work.

There's another concern...
Starship is designed to land with about 175 tons of mass
Will it stay intact at the end of the first hop if it masses 300 tons?

A few other ideas, probably stupid ones. I haven't simulated any of these...
Don't reenter the atmosphere, come down to 60 km and burn your engines to go up and change direction and the same time. The challenge with this is you have a velocity of several thousand meters per second east and you need to cancel that and go north. You probably don't have enough energy to do this.
Or you could start the reentry and use the atmosphere to lose most of your horizontal velocity, and then relight your engines to take off before you reach the surface. You have a lot of vertical velocity that you need to cancel out, and probably not enough to energy to do that.
I don't think these work either.

If we can't do it with starship, what about super heavy?
With 20 engines, super heavy can do the second hop on 235 tons of propellant, and reserving that amount leaves it with a range of 2875 km for the first hop. More than enough.
This is assuming it can handle the reentry with that much fuel, but it will have some extra fuel it could use for a reentry burn to reduce the forces it experiences.
I'm going to say that this is probably possible.

Here's a hybrid approach...
Super heavy can launch with starship on top and give it enough energy to finish the first hop. This gives plenty of margin for starship to use its engines to reenter more easily. Super heavy returns to the launch site, and then performs a later flight where it hops by itself.
This is actually practical, if you define practical as "A guy who did an amateur analysis can't come up with an obvious reason why it won't work"

What did we learn
Direct hops are possible but probably not feasible due to flightpath concerns
A hop to a floating platform and then a second hop is feasible.
A double hop with starship by itself is probably not possible
A double hop with super heavy by itself is probably possible.
A super heavy toss of starship is probably possible.
Will they do this? I have no idea.

If you liked this video please tell your friends.
